Acceleration of Gravity on an Inclined Plane

Introduction:
This lab determined the acceleration of gravity by studying the motion of a cart on an inclined track. Using Logger Pro and the graphing software the computer will collect position vs time data for the cart accelerating on the inclined track. The graph shows two accelerations which represent the time, position, and velocity of the cart as it is increasing and decreasing on the track.

Procedure:
1.)    Load logger pro on the computer and set up the track.
2.)    Incline the track by placing a small piece of wood under it near the 50 cm mark. Using a bubble level, make sure to level the track from side to side. Determine the angle of the incline by measuring the vertical and horizontal travel of the track.

B

Set the track with an incline.

3.)   Place the motion detector at the upper end of the track facing down towards the lower end. Place the cart at the bottom end and give it a gentle push uphill towards the motion detector. Prevent the cart from hitting the track to avoid damage. The cart's path should not be getting closer than 50 cm from the motion detector.
4.) After the motion detector starts to make a sound give the cart a push so it can start to collect the data. The data gets graphed by the software and from the velocity vs time graph the acceleration can be found by getting the slope of the line. 



Data:
*The next 3 graphs represent the velocity and position vs time of the cart on the first incline.

Formula to determine g
   gsin =(a1 + a2)/2
       note: a1 and a2 are the accelerations of the cart up and down the incline. 

Trial 1

The total length of the track is 228 cm with the rise of 9.55 cm. The angle of inclination can be found by getting the inverse sine of (9.55cm/228cm) = 2.4 degrees.

Trial 2

This trial's first acceleration was 0.314 m/s^2 and the second 0.400 m/s^2. This trial had g = 8.52 m/s^2.

Trial 3

The last trial for this inclined had and acceleration of 0.321 m/s^2 and 0.402 m/s^2 and g = 8.63 m/s^2

 *The next 3 graphs represent the velocity and position vs time of the cart on the second incline.

Trial 1

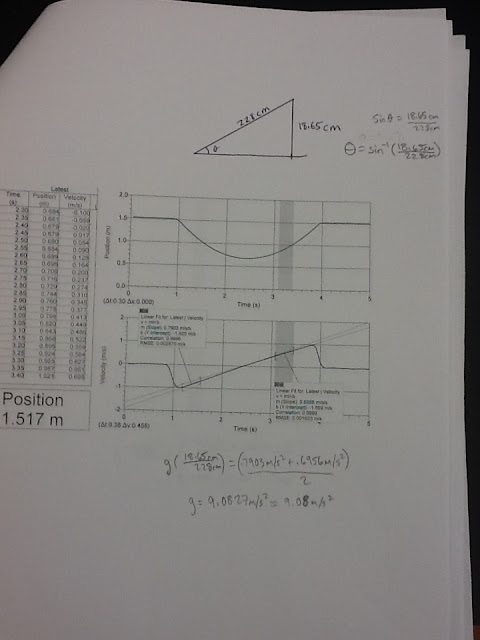The length of the graph is the same (228 cm), but the height was changed to 18.65 cm. Taking the inverse sine of the new measurements (18.65/228) gives us an angle of inclination of 4.70 degrees.

Trial 2

The first acceleration was 0.712 m/s^2, the second acceleration is 0.808 m/s^2. The second trial's g value is 9.29 m/s^2

 Trial 3

In this trial the first velocity is 0.710 m/s^2 while the second is 0.796 m/s^2 and g = 9.20 m/s^2

Conclusion:

Using an inclined track and a small cart we were able to find the acceleration of gravity. First we had to get the value of the angle of inclination using sine inverse and the known lengths of the track. Two different angles were used and each tested 3 times. The results show that our calculated acceleration for the first angle was an average of 8.54 m/s^2, off by -12.8%. The second incline had an average acceleration of 9.2 m/s^2, off by -6.2%. The second result were closer to the actual value of gravity's acceleration.